Evolving Trading Strategies With Genetic Programming - An Overview
Part 1
Writing a software program that creates - or to be more exact, evolves - trading strategies with genetic programming (GP) requires a set of design decisions to be taken concerning different aspects. In this article I will presume that the goal is to evolve a trading strategy consisting of technical indicators only, which will return entry and exit signals. Some elements like stop and limit order can be co-evolved with the basic entry and exit signals. Although it is also possible to use GP for stock selection purposes based on fundamental data, we will not look deeper into this possibility.
A complete trading strategy combines several of the following elements:
- Entry and exit indicators
- Stop loss and take profit rules
- Position sizing rules
- Emergency shutdown strategy
GP is not well-suited to cover all these elements equally. For example, having clear-cut rules when to shutdown a consistently failing strategy is a matter of monitoring one’s trading strategies and having a general money management system in place. Money management is probably the most important part of every trading stragegy, even more important than having the right exit rules in place, which in turn is more important than having the right entry rules. Money management depends on account size, personal preferences, trading style and many other variables beyond the power of GP. GP is mainly a search and optimization function, whereas proper money management requires several strategic decisions. It is a common mistake to believe that GP (or other data mining strategies) can miraculously come up with complete trading strategies on their own.
A point to consider is that evolving trading strategies with GP may not work for all markets. Some markets seem to be too efficiently priced for trading them successfully. Chen and Navet [1] describe some pretests that can be applied to the available data to distinguish in advance whether the selected market is likely to be tradeable or not.
Encoding trading strategies as rule trees
In GP trading strategies are encoded as decision rule trees. A decision rule tree is a tree-like data structure that encodes an executable algorithm. By traversing the tree from the root towards its leaves, the algorithm is executed and a result is returned from the root node. An example is given in the next figure:
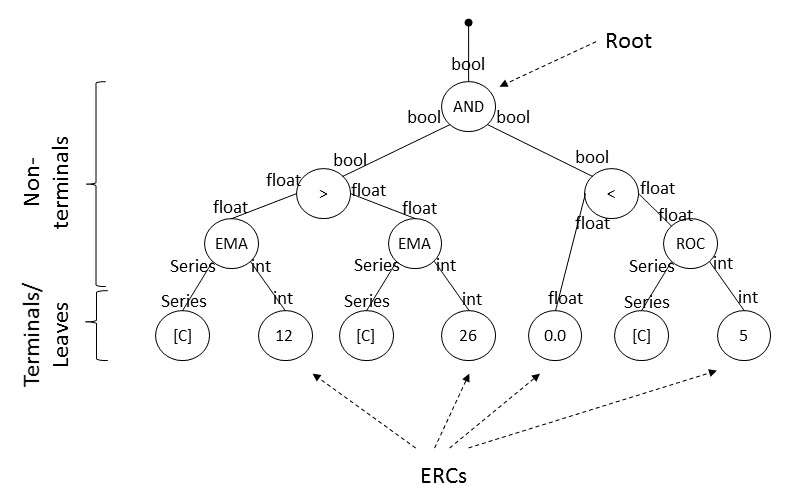
This tree encodes the following decision rule:
(EMA(Close, 12) > EMA(Close 26)) AND (0.0 < ROC(Close, 5))
The root node of the rule tree returns either true or false. In the example, EMA means exponential moving average, ROC the rate of change, and Close the series of close prices. The rule would then be: If currently not in a trade and the decision tree returns true, then enter a new long trade.
Two more remarks. First, in the figure each node has its own return type which matches the input type of another node. Terminals or leaves of course have no input nodes. This will be an important measure taken to avoid repeatedly breeding invalid rule trees. Second, ERC_s is an abbreviation for _ephemeral random constant. ERCs are leaves returning a single (often numeric) value such as an integer or a float. Handling ERCs correctly can decrease the size of the search space and thus improve search results.
Elements of Genetic Programming
Here is a list of the most important elements of every GP task:
- Data
- GP parameters and operators
- Fitness function
- Parsimony pressure
We will take a quick look into these points but leave the specifics for a series of later articles.
1. Data
GP heavily relies on existing time series data. These data must first be obtained from a data provider and be prepared manually for usage. Unfortunately, this is often a time-consuming and tedious task. Common problems are unsuitable data formats, missing data points or erroneous data. Single-stock data must be cleared for dividend payments, whereas stock index data is subject to an inherent “survivor’s bias”. A further problem is the lack of data. An often encountered rule of thumb is to have at least 10x more data points than degrees of freedom for all trading strategies tested. GP deals with multiple generations of populations of trading strategies thus magnifying the problem of sufficient data points substantially. Although the data requirements can practically never be met, nevertheless some measures can be taken to alleviate this problem.
2. GP parameters and operators
GP evolves generation after generation of populations of individuals, each individual representing one possible trading strategy. This evolutionary process relies on a set of traditional GP operators, namely:
| _Selection_ | Selects one or several individuals from a pool for a specific purpose (e.g. reproduction) by a predefined protocol |
| _Mutation_ | Creates a new individual from an existing one by creating a copy with a small, random change |
| _Crossover_ | Creates offspring from parents according to a predefined protocol |
| _Elitism_ | Allows the _n_ best individuals to directly copy themselves into the next generation |
Various implementation techniques exist for these operators, and each GP operator has different parameters to be set. Basic parameters are for instance the number of generations, the population size or the mutation probability. Parameter choices often affect the outcome of the evolutionary process in a non-linear, discontinuous way which is sometimes counter-intuitive to inexperienced users. Whereas the basic GP algorithm is actually surprisingly simple, implementing more advanced and powerful GP operators can turn out to be difficult. This is especially true if parallelism is to be used to achieve a better performance. Another common issue with more basic GP implementations is that later generations tend to fill up with identical individuals which causes the crossover and elitism operators to be ineffective.
A variety of open-source, general purpose GP implementations exist. It is often advisable to at least do some preliminary research and study their code.
3. Fitness function
As GP is ultimately simply a search or an optimization function, it needs to know what to search for or what to optimize. The fitness function assigns every individual a fitness value. Indiviuals with a better fitness value have a higher probability to survive and reproduce. In case of creating trading strategies, an obvious fitness function is to measure the (relative or absolute) monetary performance of every evolved trading strategies over a historical time period. A good trading strategy increases profits and decreases the risks taken. Again, finding a good fitness function turns out to be a common stumbling block for many developers. Most beginners start with selecting either a maximized net profit or maximized hit rate (= number of correctly predicted price movements) for fitness function. Yet, these two measures are a poor choice for various reasons that will be explained later. In most cases, having continuously positive returns is more important than achieving the highest returns. Also, more advanced fitness functions both maximize and minimize several measures at the same time.
4. Parsimony pressure
It is a well-known mathematical fact that sufficiently complicated functions can approximate literally any historical time series perfectly. (For the same reason repeatedly cunning pseudo-scientists appear in the media who claim to have successfully revealed some secret messages hidden in historical texts such as the bible. Given a sufficiently complicated search function, we can easily “discover” the Beatles song Yellow Submarine in Homer’s Odyssey.) Yet, the predictive power of these functions is nil. Without proper counter measures taken, GP has a tendency to lead to code bloat, i.e. to extremely large and complicated trading strategies with a truly wondrous performance on the in-sample data and total failure on the out-of-sample data. Parsimony pressure is applied to punish overblown complexity. Parsimony pressure is probably the most important and yet least understood concept when creating trading strategies with GP. Basically, two options exist to implement parsimony pressure: First, selecting a fitness function that assigns a low fitness to more complex trading strategies. Second, mechanically preventing the GP reproduction operators from building overly large offspring trading strategies. Since the first option alone is usually not enough to prevent code bloat, a combination of both approaches leads to an effective parsimony pressure technique.
Other articles
Next
References
[1] Chen S.-H., Navet N. (2007): Failure of Genetic-Programming Induced Trading Strategies: Distinguishing between Efficient Markets and Inefficient Algorithms. In: Computational Intelligence in Economics and Finance, Volume 2. Springer Verlag, Berlin Heidelberg. pp 169-182.
