A Short Introduction to Rhizomes
Be rk <= (ri, rj) a directed relation rk between the ordered pair of relata ri and rj, with rk ≠ ri and rk ≠ rj. We will call a relation a terminal iff ri = rj. Furthermore, we call ri (the left-hand-sided element in the ordered pair) the normative relatum and rj (the right-hand-sided element in the ordered pair) the associative relatum.
Definition:
To be really of use a rhizome must be complemented by a (bidirectional) dictionary (or similar data structure) that maps between terminals and data items. The rhizome itself does not store any data in a traditional sense, but only relations.
Here is a picture of a sample rhizome:
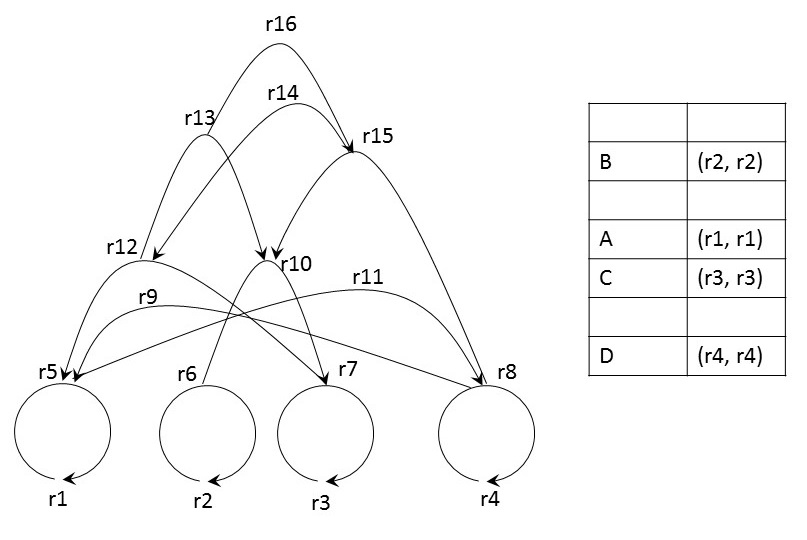
This rhizome consists of four terminal and several non-terminal relations:
| Terminals | Non-Terminals |
|---|---|
|
|
r1 to r4 are relata but not relators. Furthermore, r9, r11, r14 and r16 are only relators but not relata.
On the right-hand-side of the rhizome, we added a sample dictionary. The four characters A, B, C and D are stored in the dictionary and they were assigned a terminal relation each. The rhizome tree can be traversed from top to bottom replacing each relator through its pair of relata until all relations are resolved to terminals. Finally, the terminals are replaced with values stored in the dictionary. This is a list of relators and the character strings they represent:
- r5 <= (r1, r1) = A
- r6 <= (r2, r2) = B
- r7 <= (r3, r3) = C
- r8 <= (r4, r4) = D
- r9 <= (r8, r5) = ((r4, r4), (r1, r1)) = DA
- r10 <= (r6, r7) = ((r2, r2), (r3, r3)) = BC
- r11 <= (r5, r8) = ((r1, r1), (r4, r4)) = AD
- r12 <= (r7, r5) = ((r3, r3), (r1, r1)) = CA
- r13 <= (r12, r10) = (((r3, r3), (r1, r1)), ((r2, r2), (r3, r3))) = CABC
- r14 <= (r15, r12) = … = DBCCA
- r15 <= (r8, r10) = … = DBC
- r16 <= (r13, r15) = … = CABCDBC
It should be obvious from this simple example that relators higher up in the rhizome’s hierarchy encode longer character strings. A rhizome is not a data storage container in a traditional sense. Whereas in (unpacked) data containers a character string like DADADA contains the same characters D, A and the combination DA thereof multiple times, a rhizome is always without redundancy. At the same time, data is never simply read and retrieved from the storage system but must be regenerated for every single access.
Working with rhizomes requires the user to define a vocabulary of atomic symbols (such as the letters A to D in the example). All more complex data types (e.g. DDAC) will be combinations of these atomic symbols. As the vocabulary’s atomic data symbols are de facto immutable and because there exists always exactly one relator per ordered pair of relata, updating or deleting existing relations is - at least theoretically - not necessary.
A comparison with graphs
In computer science, a vast number of data structures are commonly represented as graphs. According to most definitions, a graph is a set of nodes (vertices) and edges (links, archs, spikes) between the nodes. Edges can be directed or undirected. Accepting such a definition for a graph, it should be noted that a rhizome is not a graph, as the only elements it consists of are relations (or directed edges). In graphs it is impossible to draw a link from one edge to another because edges are not “adressable” or “linkable”. The only way to link one edge to another is to make it a node itself. A rhizome is therefore more general or fundamental than a graph.
A further important distinction is the distinct need for storage. The storage need for a graph with a high degree of connectivity grows exponentially with an increasing number of nodes. In contrast, the required storage for a rhizome grows logarithmically with an increasing number of relations. This is because the expressive power of higher order relations in a rhizome grows exponentially, whereas it remains flat for added nodes in a graph.
