30 Oct 2014

Significance Testing of Pearson Correlations in Excel

Yesterday, I wanted to calculate the significance of Pearson correlation coefficients between two series of data. I knew that I could use a Student’s t-test for this purpose, but I did not know how to do this in Excel 2013. And, to be honest, I did not really understand the documentation of Excel’s T.TEST formula. So, here is what I did.

Pearson correlation coefficient

First, I had to calculate the corresponding Pearson correlation coefficients according to this formula:

Pearson correlation coefficient formula

where r_xy is the Pearson correlation coefficient, n the number of observations in one data series, x the arithmetic mean of all x_i, y the arithmetic mean of all y_i, s_x the standard deviation for all x_i, and s_y the standard deviation for all y_i.

Let’s assume, the data series to be correlated are stored in arrays A1:A100 and B1:B100, thus n = 100:

=PEARSON(A1:A100;B1:B100)

Alternatively, you could also use the Correl function, which returns the same result:

=CORREL(A1:A100;B1:B100)

(I am using a Swiss German localization, therefore Excel’s delimiter for formula arguments is a semicolon ; rather than a comma , in my case.)

Naturally, the returned correlation value is in the range of -1.0 to +1.0. This value is often referred to as Pearson r or r_xy in our case.

t-value

Next, I calculated the corresponding t-values according to this formula:

t-value formula

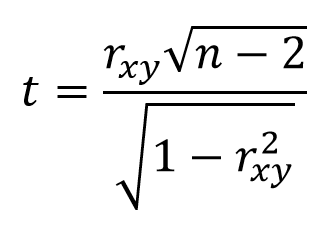
where t is the t-value, which can be positive for positive correlations or negative for negative correlations, r_xy is the already calculated Pearson correlation coefficient, and n is the number of observations again (here n = 100).

Significance testing

Finally, I needed to decide whether the computed t-values were actually significant or not. For this purpose, we need to compare them to pre-calculated t-values available in a t-value table. To do so, it is necessary to decide upon two things:

What is the desired significance or confidence level, e.g. 95% or 99%?
Do I want to use a one-tailed or a two-tailed t-test?

In my case, I decided to use a 95% significance level (which is a very common choice for data that are not highly critical). What confused me for some time is that some sources like the already linked Wikipedia-article express confidence positively by stating the degree of certainty (e.g. 0.95 or 95%), whereas others like this one express confidence negatively by the probability for being wrong (e.g. 0.05 or 5%). Other sources again like this one actually state both in a single table. It is essential that you know what the source you are using is referring to! You can always carefully compare the t-values contained in different t-tables with each other to get an understanding whether someone actually takes one or the other perspective. Just check the t-table’s header line containing the probability values. Usually, the t-values are in ascending order from left to right, and in descending order from top to bottom. Hence:

If you want to test the significance of a positive correlation, then you must check whether your t-value t is greater than a certain critical positive t-value t_crit at the right side of the t-distribution: Is t > t_crit?

If you want to test the significance of a negative correlation, then you must check whether your t-value t is below a certain critical negative t-value t_crit at the left side of the t-distribution: Is t < t_crit?

Usually, a t-table only includes positive t-values, but not negative ones. How can we then test for the significance of negative correlations? It’s really easy. t-distributions are symmetric with a median of 0, thus their left and right tails look exactly the same. For this reason, we can change our test from “Is t < t_crit?” to “Is ABS(t) > t_crit?”. Instead of checking whether our t-value is below a critical negative threshold, we actually check whether its absolute value is greater than a critical positive threshold.

In case you do not have a very clear idea whether the expected correlation is actually positive or negative because it could be both it is better to use a two-tailed t-test. You can use a one-tailed t-test if you are only interested in one directionality of the correlation but not in the other (e.g. only positive but not negative, or only negative but not positive). Always remember:

The probability value of a two-tailed t-value is 2x the probability value of a one-tailed t-value:

p(t) two-tailed = 2 * p(t) one-tailed

The t-table contains in the first column the degrees of freedom. This is usually the number of observations n (i.e. 100) minus some value depending on the context. When computing significances for Pearson correlation coefficients, this value is 2: degrees of freedom = n - 2.

We now have all information needed to perform the significance test. i) We have decided upon a confidence level of 95%, ii) we have decided to use a two-tailed t-test, iii) we have calculated the degrees of freedom to be 98 = 100 - 2. Looking up the critical threshold t_crit in the t-table we find that it is 1.984. Therefore:

If r_xy > 0 AND t > 1.984 then the Pearson correlation coefficient is significantly positive. This would be reported more compactly as: r_xy(98) = <value>, p < 0.05 (two-tailed), where <value> is of course the calculated Pearson correlation coefficient.
If r_xy < 0 AND ABS(t) > 1.984 then the Pearson correlation coefficient is significantly negative.
In all other cases the result is not significant.

Using Excel for t-tests

TINV, T.INV.2T, TDIST, and T.DIST.2T

Of course, calculating critical t-values can be done in Excel too. Before Excel 2010, there were only the TINV and TDIST formulas, now there are additionally the T.INV.2T and the T.DIST.2T formulas. All these formulas express confidence negatively, that is the probability value p represents the probability for being wrong.

`=TINV(p;df)`	returns a t-value t for the given probability p and degrees of freedom df, assuming a two-tailed test. `=TINV(p;df)` is equivalent to `=T.INV.2T(p;df)`.
`=T.INV.2T(p;df)`	returns a t-value t for the given probability p and degrees of freedom df, assuming a two-tailed test. `=T.INV.2T(p;df)` is equivalent to `=TINV(p;df)`.
`=TDIST(t;df;num-tails)`	returns a probability value p for the given t-value t, the degrees of freedom df, and the number of tails num-tails (either 1 or 2). `=TDIST(t;df;2)` is equivalent to `=T.DIST.2T(t;df)`. Furthermore, `=2*TDIST(t;df;1)` is equivalent to `=T.DIST.2T(t;df)`.
`=T.DIST.2T(t;df)`	returns a probability value p for the given t-value t, the degrees of freedom df, and a two-tailed t-test. `=T.DIST.2T(t;df)` is equivalent to `=TDIST(t;df;2)`.

TINV is the inverse of the TDIST formula and vice versa.

Examples: Let p = 0.05 (5% probability of being wrong), n = 100 (therefore df = 100 - 2 = 98). We assume a two-tailed t-test.

Calculating t for a given p: =TINV(0.05; 100-2) = =T.INV.2T(0.05; 100-2) = 1.9844675.
Calculating p for a given t: =TDIST(1.9844675;100-2;2) = =T.DIST.2T(1.9844675;100-2) = =2*TDIST(1.9844675;100-2;1) = 0.05.

T.INV and T.DIST

Since Excel 2010, there is also a T.INV and a T.DIST formula. Confusingly, they actually work quite differently from TINV and TDIST! First, unlike TINV and TDIST, T.INV and T.DIST by default are one-tailed. Second, unlike TINV and TDIST, T.INV and T.DIST actually express confidence positively, that is the probability value p represents the degree of certainty.

`=T.INV(p;df)`	returns a t-value t for a given probability p and degrees of freedom df, assuming a one-tailed test. `=T.INV(p;df)` is equivalent to `=TINV(2*(1-p);df)`.
`=T.DIST(p;df;true)`	returns a probability value p for the given t-value t, the degrees of freedom df, assuming a one-tailed t-test. `=2*(1-T.DIST(p;df;true))` is equivalent to `=TDIST(p;df;2)`. Furthermore, `=1-T.DIST(p;df;true)` is equivalent to `=TDIST(p;df;1)`.