Implementing a Fixed-Length FIFO Queue in Java
When working with time series data, one often needs to calculate sums of consecutive numbers for a predetermined time frame. Imagine for example calculating a moving average with a fixed size. Let’s look at a very simply time series.
[0 |1 |2 |3 |4 |5 |6 |7 ]Assuming a moving average of length 4 results in the following array:
[x |x |x |1.5|2.5|3.5|4.5|5.5]The formula for a moving average of length 4 thus is:
MAt = (Sum of all elements from t-3 to t) / 4
How would we efficiently implement this in Java code? The problem is that we need to calculate the Sum in the formula for every moving average. Of course it is possible to always reiterate over all numbers in the current time frame to do so, but this is unnecessarily slow. Instead, we can simply subtract the last element in the time frame and add the newest one to Sum. In this way we can save a significant number of unnecessary computations. Still we have to keep track of what actually are the old and the new elements. We have to store these numbers somewhere. An appropriate data structure would be a first-in-first-out (FIFO) queue of numbers. But how exactly can a FIFO queue be implemented in a (non-functional) programming language such as Java? The first idea is typically to use an array-based implementation and to shift the position of elements in the array by repeatedly creating slightly shifted copies of the array. In the above example, we would need to create a new array five times, once for every new Sum being calculated. This is of course very inefficient, because creation of an array in memory is relatively slow. Implementations based on classes such as java.util.ArrayList or java.util.Vector are already much better, because internally they rely on longer arrays and indices. Still this is not the best solution, because once the internal indices move outside the internal array’s boundaries a new copy of the internal array must be created.
A typical alternative for implementing FIFO queues is thus using a linked list:
[0-> 1-> 2-> 3-> 4-> 5-> 6-> 7]The advantage is obvious, no more copying or re-creating arrays in memory. All we have to do is manipulating a few pointers. Of course we lose the advantage of directly assessing an element in the queue by index, but for our purpose - calculating moving averages - this is something we do not want to do anyway.
Yesterday, it suddenly occurred to me that there is actually an even better alternative if the length of the queue is fixed (as in our example). We can effectively use a ring.
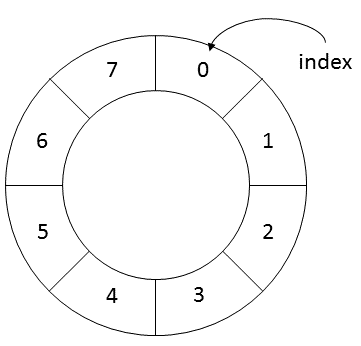Adding a new number to the queue and dropping the oldest one is the same as simply replacing the oldest element in this ring with a new one. Internally, we can again use an array of a fixed length in combination with a rotating index. This is how the code looks like in Java. First, let’s create our own Queue interface:
public interface Queue<E> {
public boolean add(E e);
public E element();
public boolean offer(E e);
public E peek();
public E poll();
public E remove();
}This interface deviates somewhat from the one provided in the Java libraries but this is unimportant for now. Next, the implementation of our queue:
public class NumberFixedLengthFifoQueue implements Queue<Number> {
protected Number[] ring;
protected int index;
/**
* @param initialValues contains the ring's initial values.
* The "oldest" value in the queue is expected to reside in
* position 0, the newest one in position length-1.
*/
public NumberFixedLengthFifoQueue(Number[] initialValues) {
// This is a little ugly, but there are no
// generic arrays in Java
ring = new Number[initialValues.length];
// We don't want to work on the original data
System.arraycopy(initialValues, 0, ring, 0, initialValues.length);
// The next time we add something to the queue,
// the oldest element should be replaced
index = 0;
}
@Override
public boolean add(Number newest) {
return offer(newest);
}
@Override
public Number element() {
return ring[getHeadIndex()];
}
@Override
public boolean offer(Number newest) {
Number oldest = ring[index];
ring[index] = newest;
incrIndex();
return true;
}
@Override
public Number peek() {
return ring[getHeadIndex()];
}
@Override
public Number poll() {
throw new IllegalStateException("The poll method is not available for NumberFixedLengthFifoQueue.");
}
@Override
public Number remove() {
throw new IllegalStateException("The remove method is not available for NumberFixedLengthFifoQueue.");
}
@Override
public Number get(int absIndex) throws IndexOutOfBoundsException {
if (absIndex >= ring.length) {
throw new IndexOutOfBoundsException("Invalid index " + absIndex);
}
int i = index + absIndex;
if (i >= ring.length) {
i -= ring.length;
}
return ring[i];
}
@Override
public String toString() {
StringBuffer sb = new StringBuffer("[");
for (int i = index, n = 0; n < ring.length; i = nextIndex(i), n++) {
sb.append(ring[i]);
if (n+1 < ring.length) { sb.append(", "); }
}
return sb.append("]").toString();
}
protected void incrIndex() {
index = nextIndex(index);
}
protected int nextIndex(int current) {
if (current + 1 >= ring.length) { return 0; }
else return current + 1;
}
protected int previousIndex(int current) {
if (current - 1 < 0) { return ring.length - 1; }
else return current - 1;
}
protected int getHeadIndex() {
if (index == 0) { return ring.length-1; }
else return index-1;
}
}The queue “rolls” through the ring. Adding a new element at the head of the queue automatically removes the oldest element in the queue - no copying of arrays or resetting of object references required. Unlike with linked lists we can actually access each element in the ring directly with the get method. Finally, we can create a subclass of our queue object which will graciously roll over as new values are added into the queue/ring.
public class RollingMovingAverage extends NumberFixedLengthFifoQueue {
private float maNumerator;
private float maValue;
public RollingMovingAverage(Number[] initialValues) {
super(initialValues);
maNumerator = 0.0f;
maValue = 0.0f;
initialize();
}
public float getValue() {
return maValue;
}
@Override
public boolean add(Number newest) {
return this.offer(newest);
}
@Override
public boolean offer(Number newest) {
maNumerator -= ring[index].floatValue();
boolean res = super.offer(newest);
maNumerator += ring[getHeadIndex()].floatValue();
maValue = maNumerator / (float) ring.length;
return res;
}
private void initialize() {
for (int i = previousIndex(index), n = 0; n < ring.length; i = previousIndex(i), n++) {
maNumerator += ring[i].floatValue();
}
maValue = maNumerator / (float) ring.length;
}
}We can use the class now. The length of the moving average is initially set through the length of the array given to its constructor.
Integer[] initialMovAvgFrame = { 0, 1, 2, 3 };
RollingMovingAverage ma = new RollingMovingAverage(initialMovAvgFrame);
ma.getValue(); // returns 1.5
ma.add(4);
ma.getValue(); // returns 2.5
ma.add(-1);
ma.getValue(); // returns 2