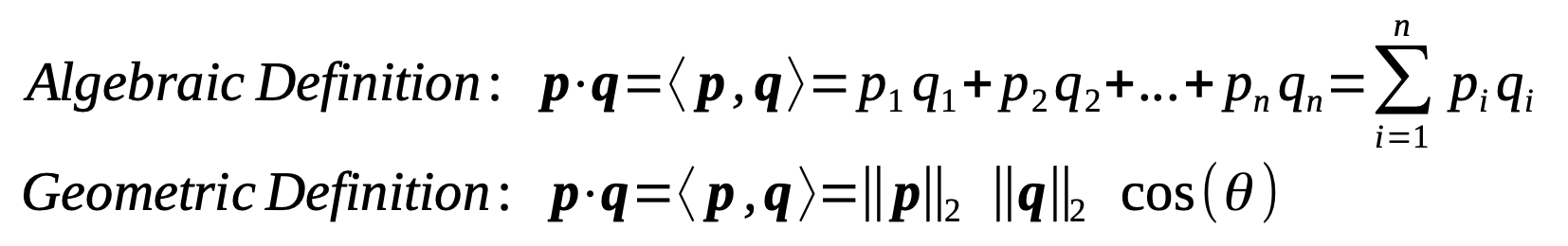Basics of vector algebra
Understanding vector algebra is a prerequisite to selecting meaningful distance metrics for text embeddings. For the fun of it, let’s recall some of the basics.
Basics of vector algebra
Let p and q be each a n-dimensional vector in a n-dimensional Euclidean space.
Addition and subtraction of vectors
Addition and subtraction of vectors of equal length is quite straight forward. Both operations produce a new vector with same number of components.
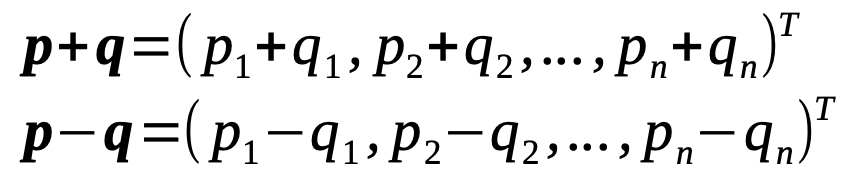
Norms of a vector
The “length” or “magnitude” of a vector can be defined for a vector in various ways, we must at least distinguish between the level 1 and level 2 norms.
Level 1 Norm
Level 1 Norm (L1) is the sum of the absolute values of the vector’s components.
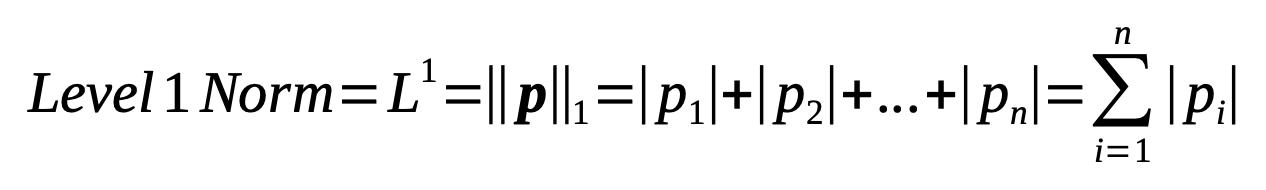 The level 1 norm is always a scalar number, i.e. a singular value. For real valued vectors it cannot take a negative value, and it can only be 0 when all its componenrts are 0.
The level 1 norm is always a scalar number, i.e. a singular value. For real valued vectors it cannot take a negative value, and it can only be 0 when all its componenrts are 0.
Level 2 norm (Euclidean norm)
Level 2 Norm (L2) or also called Euclidean Norm is the square root of the sum of the squared (absolute) values of the vector’s components.
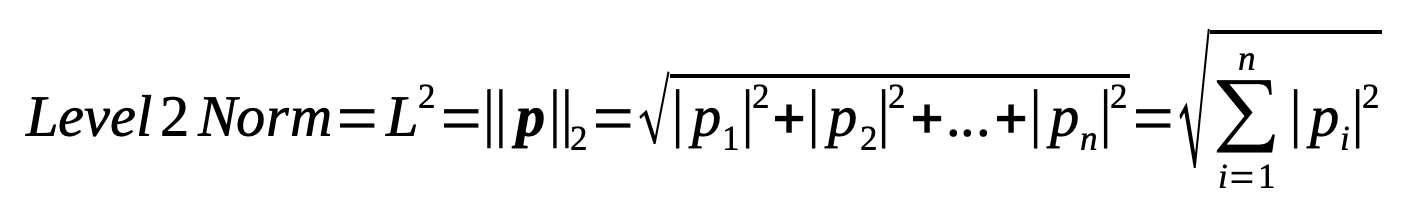 The level 2 norm is always a scalar number, i.e. a singular value. For real valued vectors it cannot take a negative value, and it can only be 0 when all its components are 0.
The level 2 norm is always a scalar number, i.e. a singular value. For real valued vectors it cannot take a negative value, and it can only be 0 when all its components are 0.
Note that in some cases the L1 norm is also written as |p| and the L2 norm as ||p|| without the extra subscript. The L2 norm is so common that it is often referred to simply as “the norm” without indicating that the L2 norm is referred to rather than L1 norm.
Generalized norm
Besides L1 and L2, in principle we can also calculate L3, L4 and even L∞ norms. We can generalize the above formulas to the following one:
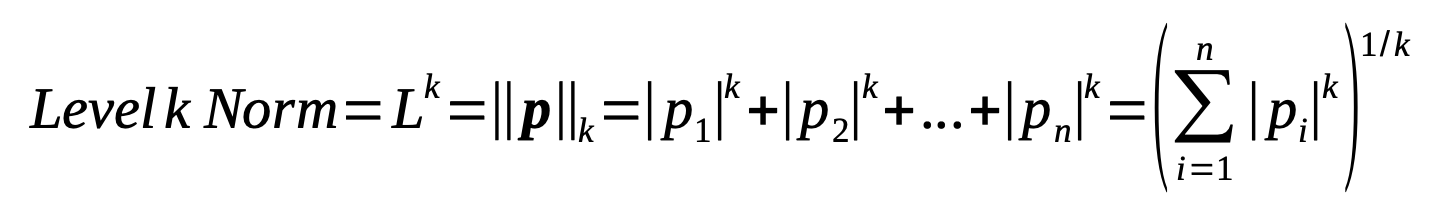
Multiplication of vectors
Vectors can be multiplied in different ways, the most basic ones are the scalar multiplication and the dot product. Another relatively common multiplication is the cross product (also called vector product).
Scalar multiplication
The scalar multiplication is a multiplication of a vector p with a single number c. Scalar multiplication always returns a vector with the same number of components as the original. Geometrically speaking this can be interpreted as a re-scaling of the vector’s length (it can even make it point in the opposite direction thus returning the inverse vector) but beyond that does not change its fundamental directionality.
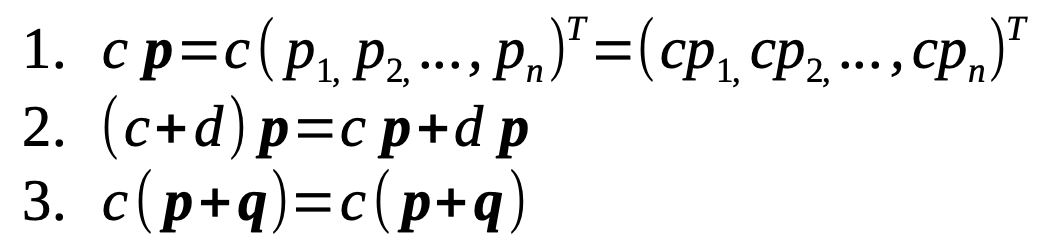 Scalar multiplication with 0 returns the somewhat boring 0 vector: 0 p = 0.
Scalar multiplication with 0 returns the somewhat boring 0 vector: 0 p = 0.
Element-wise multiplication
The Hadamard product or also called element-wise multiplication is a component by component multiplication of two vectors p and q with n dimensions. Element-wise multiplication returns a vector with the same dimensionality as the two originals. Giving a geometric explanation is tricky, so I will skip this here. Its definition on the other hand is quite simple.
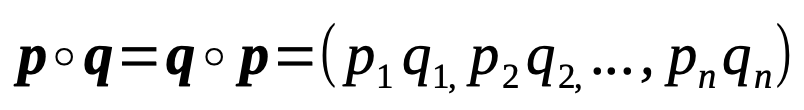
Dot product
The dot product (also called scalar product) is a multiplication of two vectors p and q of same dimensionality. Algebraic dot product as expressed by me:
The [algebraic] dot product of two vectors can be defined as the sum of all multiplied components of two vectors.
Geometric dot product as expressed by Wikipedia:
The [geometric] dot product of two vectors can be defined as the product of the magnitudes of the two vectors and the cosine of the angle [θ] between the two vectors.
As you can see there exists both an algebraic and a geometric version of the dot product. You can find a mathematical proof online in various places that the two indeed lead to same results, i.e. algebraic dot product = geometric dot product. The dot product is very important. It contains information about the angle (θ) between two vectors. If they are orthogonal to each other then the dot product is 0. If they are pointing into the same direction, i.e. when they are parallel) the dot product will be as positive as it gets. If they point into the opposite direction (also parallel to each other) the dot product will be as negative as it gets. (By the way, many math libraries require the angle θ to be converted into a radians number before entering it as a parameter to the cosine function.)
Did you also notice what I just claimed in above formula? I wrote: p∙q = <p,q>. This means: The dot product of two vectors p∙q is equal to their inner product <p,q>. This rule generally works for the text embedding algorithms I’m familar with, but if we want to be very precise then the inner product might be defined differently than the dot product, especially if you are leaving the world of Euclidean spaces. See here and here. (Don’t worry, we won’t dive into such territory here.)
We can also rewrite the geometric interpretation of the dot product formula to calculate the angle θ by its vectors:
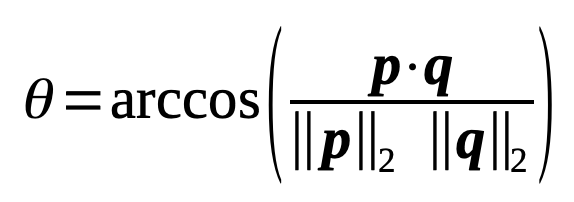
Cross product
The cross product (also called vector product) is also a multiplication of two vectors of same dimensionality, but a different one than the dot product. It is only defined for vectors with at least 3 components, i.e. it cannot be applied in 1- or 2-dimensional Euclidean spaces. (The following formula gives the algebraic definition for 3 dimensions only.)
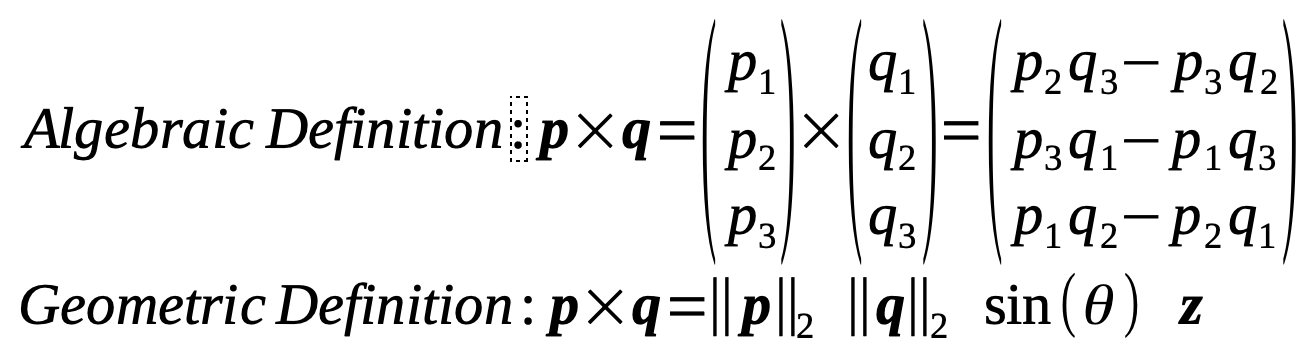 The new vector z (also often denoted as n) is the unit vector that is orthogonal to the planar area spanned by vectors p and q. A unit vector has a magnitude (L2 norm) of 1, i.e. ||z||2 = 1. Multiplication with z ensures that the cross product vector points into the “right” direction. The geometric version of the cross product is usually used to determine the angle θ between two vectors, that is not in the form written above. As it is of less importance to my concerns (text embeddings!) I don’t want to go into details. You can find a short introduction for 3D spaces here, a nice video illustration on Wikipedia, and a short discussion on how to generalize to more dimensions on Stackexchange.
The new vector z (also often denoted as n) is the unit vector that is orthogonal to the planar area spanned by vectors p and q. A unit vector has a magnitude (L2 norm) of 1, i.e. ||z||2 = 1. Multiplication with z ensures that the cross product vector points into the “right” direction. The geometric version of the cross product is usually used to determine the angle θ between two vectors, that is not in the form written above. As it is of less importance to my concerns (text embeddings!) I don’t want to go into details. You can find a short introduction for 3D spaces here, a nice video illustration on Wikipedia, and a short discussion on how to generalize to more dimensions on Stackexchange.
We could also say that the dot product focuses interactions of vector components in the same dimension, whereas the cross product focuses on vector components in distinct dimensions. (More explanation here.)
Division of vectors
Logically speaking, division of vectors should be the inverse to multiplication, no? Immediately questions arise. As we have seen, there are at least three different types of multiplication.
Division by a scalar
Division of a vector by a scalar is rather simple - as long as the scalar is not zero! In fact, we could redefine division by a scalar as multiplication with 1/scalar (where scalar ≠ 0). Thus:
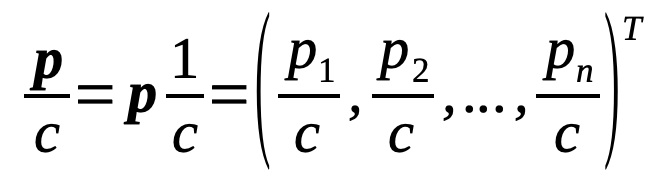
Element-wise division?
Element-wise division is already more complicated. In theory, this could be achieved as long as the divisor vector does not contain any elements that are zero. In reality however this is much harder to control than when dividing by a scalar. So, we won’t pursue this any further.
Division for inverse of dot and cross product?
And, what about division as the inverse of the dot and cross product? Setting the potential problem of division by zero aside for a moment, it turns out such a thing does not exist (see e.g. here or here or here).
Vector unit-normalization
A (non-zero) vector’s length can be unit-normalized. The result is a (rescaled) vector of same dimensionality as the original with magnitude (L2 norm) of 1. The new vector is called a “unit vector” or “normalized vector”. Note that we divide each component of p with the scalar p’s magnitude. Hence, ||p̂||2 = 1.
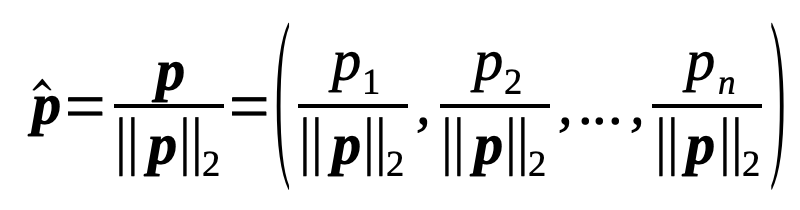
Similarity and distance measures for two vectors
When working with text embeddings a common need is to measure the (dis-) similarity or distance between two vectors. In text embeddings a very common problem is to find the nearest neighbours of a given vector: Which out of all my other vectors are the most similar to a given vector? To answer this question we first have to establish a distance or similarity measure. We will continue to operate in an Euclidean space only, many other distance measures exist in non-Euclidean spaces that are of no concern here. So, let’s look into two extremely popular distance/similarity measures, the Euclidean distance and the cosine similarity.
Euclidean distance
Remember that in an Euclidean space we can understand a given pair of Cartesian coordinates as either coordinates, or alternatively, as vectors from the origin to the coordinates? For example, in a 2d-space where we have the coordinates p = (1, 5) and q = (4, 3) we could interpret the coordinates p and q also as vectors p = ((0,0), (1,5)) and q = ((0,0), (4,3)). Therefore, in Euclidean space, we can interpret the distance between p and q in two different ways - either as a distance between Cartesian coordinates p and q or as a distance between two vectors p and q. Calculating the distance between two coordinates in a 2d-space is something we learned in high-school using Pythagorean maths where a2 +b2 = c2 for a triangle with a right angle betwee a and b.
distance(p, q) = sqrt( (4-(-1))^2 + (3-5)^2 ) = sqrt(29)
The Euclidean distance is nothing but a generalization of this formula to n dimensions. Letl q - p be the so called displacement vector between p and q, that is a vector pointing from coordinate p to q. Thus:
q - p = (q1 - p1, q2 - p2, …, qn - pn)
We have already seen how we can measure the length of a vector by it’s Euclidean or L2 norm. Thus, the length or magnitude of the vector between coordinate p and q is nothing but the L2 norm of the displacement vector q - p, that is | |q - p | |. Furthermore, as it is a length measure it does not really matter whether we calculate the distance between p and q or q and p, and therefore | |q - p | | = | |p - q | |.
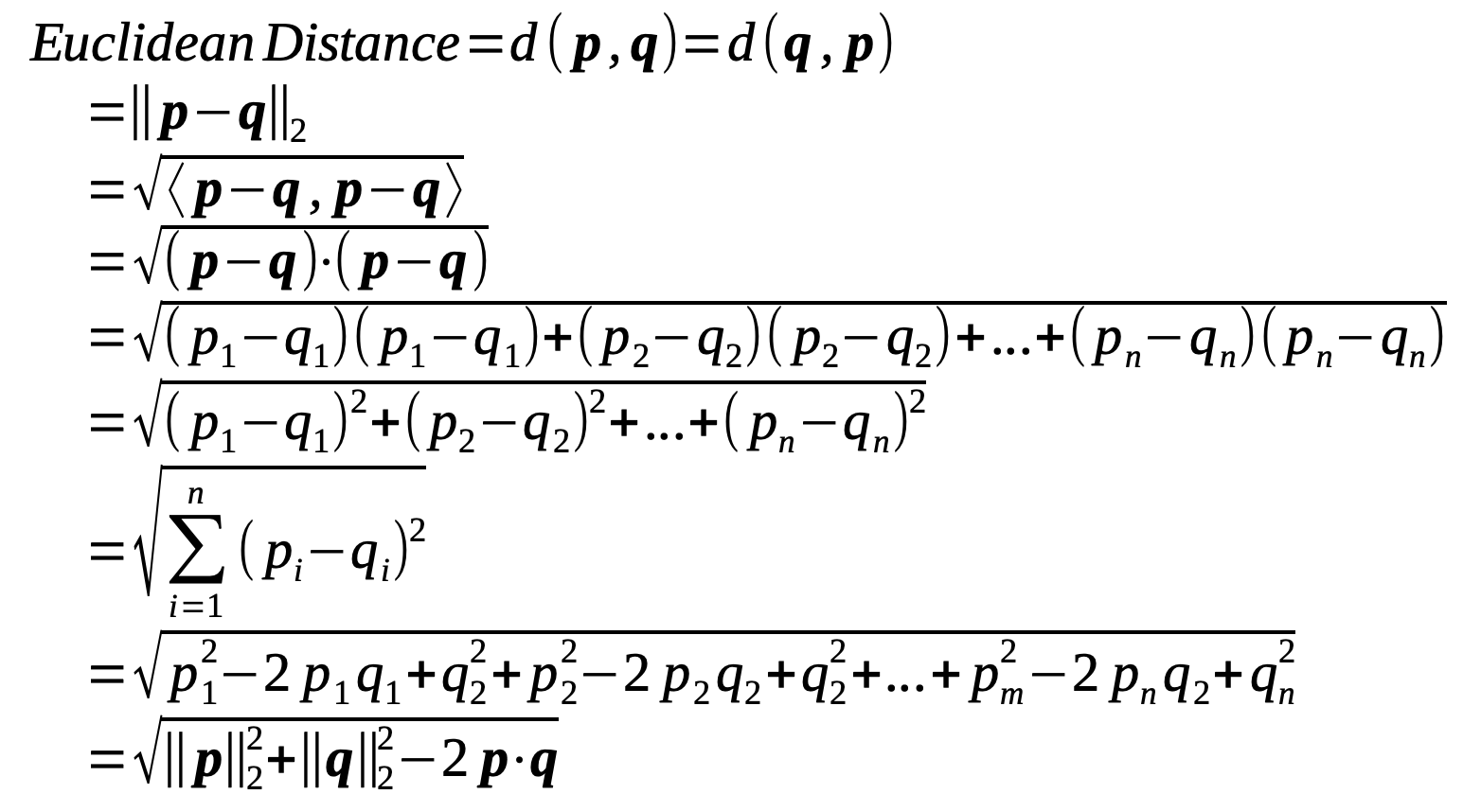
As you can see from the formula the Euclidean distance is the square root of the inner product of p - q (and also of q - p). Since we are using the dot product as the inner product, it turns out that the Euclidean distance is same as the L2 norm (Euclidean norm) | |p - q | |. The last two lines give a different style of writing again.
The Euclidean distance is always a non-negative number. If two vectors are identical, it is 0. The higher the Euclidean distance, the further two coordinates and thus their vectors are apart.
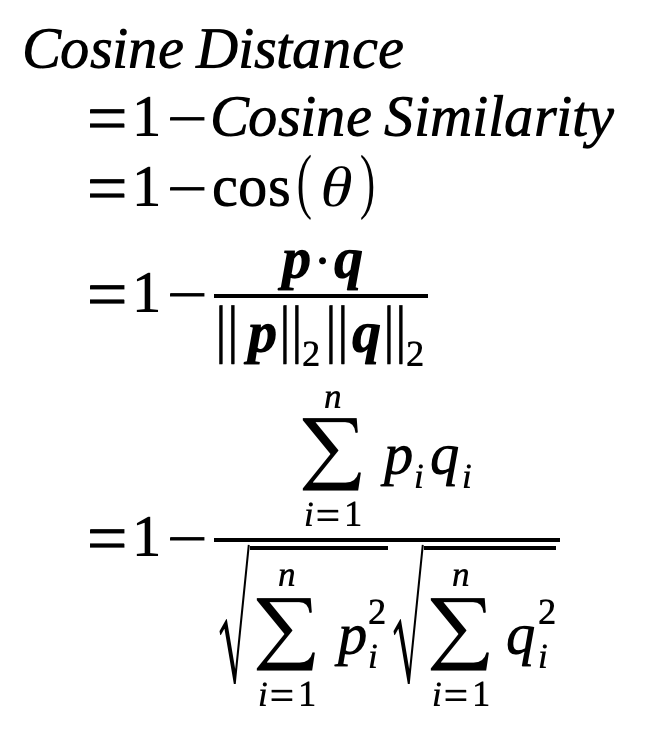
Cosine similarity and cosine distance
A different distance way to measure similarity (and thus distance) between two vectors is to look solely at the angle θ occurring between two vectors. The definition of the cosine similarity of the angle can be derived very simply from the above mentioned definition of the dot product. The relation between cosine similarity and cosine distance is simply cosine distance = 1 - cosine similarity. Thus, the cosine distance is defined in a range [0, 2], whereas the cosine similarity is defined in a range [-1, 1].
| Angle | Cosine Similarity | Cosine Distance | Geometric Interpretation |
|---|---|---|---|
| 0° | 1 | 0 | Overlapping vectors with same directionality |
| 90° | 0 | 1 | Orthogonal vectors |
| 180° | -1 | 2 | Vectors pointing into opposite directions |
| 270° | 0 | 1 | Orthogonal vectors again |
| 360° | 1 | 0 | Overlapping vectors with same directionality |
Comparison of Euclidean and cosine distance
Whereas the Euclidean distance depends on the vectors’ magnitude and also the angle between the vectors, the cosine distance only depends on the angle but not on the magnitudes. This is an important difference between the two distance metrics.
However, when we unit normalize all our vectors then the Euclidean and the cosine distance fall together! Geometrically speaking unit normalized vectors have the same (L2) magnitude of 1. Thus, the distance between their coordinates directly correlates with the angle between the vectors, and therefore the Euclidean distance and the cosine distance are correlated with each other.
Further resources
General introduction:
Dot and cross product:
- Understanding the Dot Product and the Cross Product by Joseph Breen
- https://betterexplained.com/articles/cross-product/
- https://en.wikipedia.org/wiki/Cross_product
- https://www.mathsisfun.com/algebra/vectors.html
- https://www.mathsisfun.com/algebra/vectors-cross-product.html
Difference between dot product and inner product:
Unit vector:
- Stackexchange discussion on unit vector in cross product
- Another Stackexchange discussion on the role of the unit vector in cross product
- https://www.khanacademy.org/computing/computer-programming/programming-natural-simulations/programming-vectors/a/vector-magnitude-normalization
Eudlicean versus cosine distance: