Rhizomes as transistors

There is a natural similarity between a rhizome’s relation and how modern transistors work. As it turns out, we could actually build a rhizome (with limitations) using transistors. Have a look at the following example. Every transistor consists of a collector, an emitter and a base.

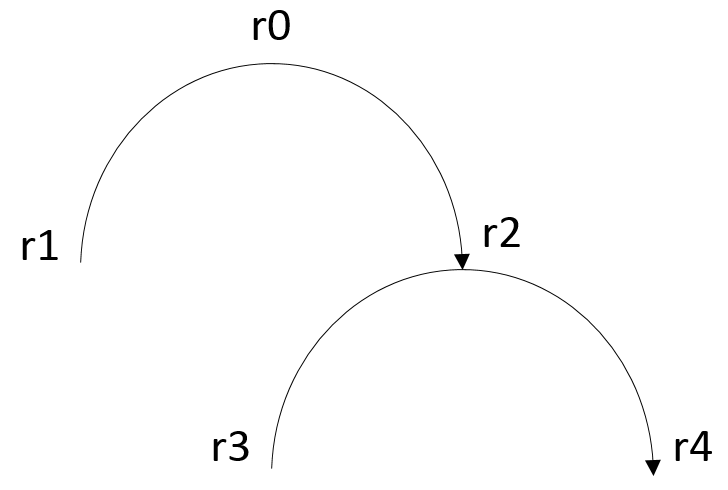
• r2 <= (r3, r4): We will call relatum r3 the collector, and relatum r4 the emitter. Another relation’s emitter, r2, will act as the base.
• r0 <= (r1, r2): A second relation is used to act as the base for r2. Note that this relation again can be understood as consisting of a collector r1 and an emitter r2, yet without a base.

Every relation can either conduct a current (it can “fire”, if we want to use more neuroscience terms) or not.

#Building a NOT-gate (inverter) with rhizome relations How then can we use a rhizome to compute? Well, knowing really just the basics of electronics is sufficient to understand the basics.

By adding more relations, we can actually build a NOT-gate (inverter). Let’s assume the same relations as before. This time, we however add two more relations.

• r2 <= (r3, r4): With r3 being the collector, r4 the emitter and r2 the place where the base is attached. The base itself is again represented as r0 <= (r1, r2).
• r6 <= (r3, r7): With r3 being the collector, r7 the emitter and r6 the place where the base is attached. The base itself is again represented as r5 <= (r1, r6).

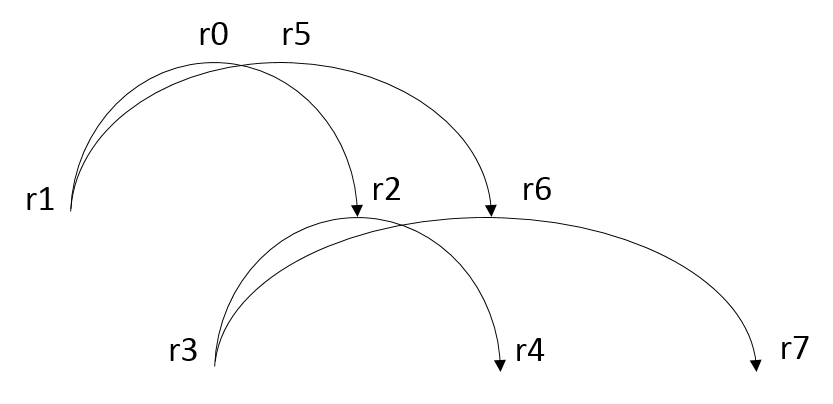
In the collector r1 we either conduct a current through r0 to emitter r2, or we conduct a current through r5 to emitter r6. At the same time, we conduct a current from collector r3 through r2 to emitter r4 as well as from r3 through r6 to emitter r7. Depending on which base is currently active, either r4 or r7 will be active, but not both at the same time. Hence, we have created a simple logical NOT gate.

Now, the situation is actually not as simple as I just described. In a way I tricked a little. I have left two questions unanswered so far: First, how is it decided in collector r1 whether to conduct a current through one or the other relation? Second, what if suddenly a current would be conducted (or not conducted) through both relations at the same time?
To answer the first question: The decision to either activate one or the other relation r0 <= (r1, r2) or r5 <= (r1, r6), i.e. the “base relations” from the perspective or r2 and r6, is not stored or controlled from inside the depicted rhizome at all. It must actually be the application’s responsibility to decide how/when to switch conducts between one or the other base relation. In the simplest possible case we can use another existing common hardware NOT gate that can produce exactly one or another output (but not both at the same time).
In a more sophisticated world however we could separate the two decisions whether to activate one or the other relation. They could then be activated independently of each other. This immediately leads to an interesting paradoxon: the emittors r4 and r7 could potentially be activated or deactivated at the same time. In other words, the system would at the same time produce two output signals that is a value and its negation, for example true and false (or alternatively false and true) concurrently. From the perspective of traditional boolean logic this makes no sense at all. First, something and its negation cannot coexist, it’s either one or the other and nothing else (law of excluded third). Second, there can not be two values at the same time (law of noncontradiction). Yet, this is exactly what our rhizome produces in such a situation. So, what do we make of it?
I will skip the philosophical questions that may arise and focus only on the technical aspects. Basically, what is required is a strategy to handle such situations. Note that no such strategy is predefined anywhere in the existing rhizome, so the strategy must again come from the outside, it cannot be predetermined by the rhizome itself. Unfortunately, I must leave the question unanswered where this strategy actually comes from or how it’s represented exactly as this is not entirely clear to me neither at this point. The goal must be to establish one or several new relations of higher order than the existing relations which actually determine how the situation must be handled. For example, the strategy may establish a new relation r8 <= (r0, r5) or r8 <= (r5, r0), or maybe a relation between r2 and r6, or perhaps directly between r4 and r7. Whenever an unprecedented or contradictory situation occurs new relations are added to the rhizome to handle exactly this situation. Perhaps new relations could be added randomly, and those that are unused for some time or that do not lead to successful strategic behaviour are eventually forgotten. Whatever the case, as a consequence the rhizome grows in size over time. Yet, relations of higher order tend to also handle more complexity, so assuming a relatively constant exposure to outside stimuli the growth should follow a logarithmic pattern.